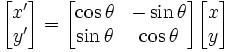[ rotace | interpolace | výpočet parametrů | zadání ]

Geometrické transformace – rotace

V tomto cvičení se budeme zabývat (globálními) geometrickými transformacemi obrázku. Budeme tedy posouvat souřadnice jednotlivých bodů, nikoli jejich jasové hodnoty. Globální znamená, že jednu tranformaci aplikujeme na všechny souřadnice obrazu. Takové tranformace nacházejí velmi široké uplatnění při úpravách fotografií a lze je provádět interaktivně s použitím např. programu GIMP.

Pro jednoduchost se zaměříme na rotaci. Vlastní transformace obrazu má dvě části: transformaci souřadnic bodů a interpolaci jasu v nich. Pokud se snažíme o rektifikaci obrazu do referenčního souřadného systému, musíme nejprve potřebnou transformaci vypočítat.

Rotace

Transformaci souřadnic [x y]' rotací okolo počátku o úhel θ v kladném směru otáčení lze popsat maticově:

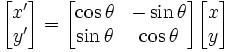
Zamyslete se, zda v našem případě stačí rotace okolo počátku. Kladný směr otáčení je definován od kladné první osy ke kladné druhé ose (v našem případě od x k y). Nezapomeňte, že v obraze má osa y opačný směr.

Všimněte si, že jediným maticovým násobením lze transformovat N bodů, stačí je zapsat do jedné matice velikosti 2×N. Kromě lepší přehlednosti to v MATLABu přináší zrychlení oproti cyklu.

Pro vytvoření rotovaného obrazu potřebujeme:

  1. znát velikost, kterou nový obraz v neotočené 2D mřížce zabere
  2. znát souřadnice bodů v mřížce lze použít funkci meshgrid()
  3. vypočítat, které původní souřadnice odpovídají souřadnicím v mřížce (zpětná transformace)
  4. interpolovat hodnoty z původních dat

Interpolace

MATLAB nabízí pro interpolaci funkci interp2(), kde lze pomocí parametrů vybrat metodu. Implementaci nejjednodušší metody nearest neighbor si můžete vyzkoušet sami.

Výpočet parametrů transformace

Zatím jsme předpokládali znalost parametrů transformace, tu ale například při narovnání našikmo pořízené fotografie předem nemáme. Pokud ale obraz obsahuje výrazné paralelní hrany, které chceme natočit do určitého úhlu můžeme Radonovou transformací (doc radon) ve výkonovém spektru nalézt nejčastěji zastoupený směr hran. Rotaci stačí spočítat jako rozdíl mezi tímto a požadovaným směrem.

vstup log(im_Pfft) Radonova transformace hodnoty odpovídající
projekcím počátkem

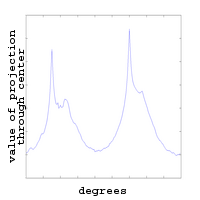
Radonova transformace – zjednodušené vysvětlení

Radonova transformace provádí 2D→1D projekci intenzit v obraze pod různými úhly. Představte si vodorovné přímky vedené každým řádkem obrazu. V prvním kroku sečteme intenzity podél každé přímky a výsledek uložíme do prvního sloupce výstupní matice. V druhém kroku pootočíme přímky o zadaný úhel, sečteme intenzity podél nich, a výsledek uložíme do druhého sloupce. Takto postupujeme pro zadaný rozsah úhlů, v MATLABu defaultně 0:179 stupňů. Stejnou 2D→1D projekci se změnou úhlu provádí rentgen v počítačové tomografií (CT). My Radonovu transformaci použijeme pro nalezení přímky s nejvyšší intenzitou.

Zadání:

Váš kód bude otestován automaticky na sadě obrazů, které nebudete mít při vývoji k dispozici. Je proto důležité:

  1. Implementujte funkci theta = estimaterotation(I), kde I je dvourozměrná matice typu uint8 reprezentující šedotónový obraz s výraznou pravoúhlou strukturou, vychýlenou max. o ±40 stupňů od os obrazu. Výstup theta udává, o jaký úhel (ve stupních v kladném směru x→y) je nutné fotografii otočit, aby struktura souhlasila s osami obrazu. Např. pro tuto fotografii theta = -10.

  2. Implementujte funkci R = rotationmatrix(theta), která vytvoří rotační matici R 2×2 pro úhel theta stupňů.

  3. Implementujte funkci Ir = rotateimage(I,R), která provede rotaci obrazu zadanou rotační maticí R a vrátí výsledek jako dvourozměrnou matici Ir typu uint8. Nesmí dojít k oříznutí obrazu ani přidání zbytečných okrajů – vypočtěte přesně velikost vzniklého obrazu. Očekáváme vaši vlastní implementaci metody nearest neighbor, nepoužívejte funkce interp2, imrotate, imtransform nebo tformarray.

Každý krok je hodnocen nezávisle.

Prezentace a cvičení převzaté od Ing. Tomáše Svobody, PhD, ČVUT Praha, upravil doc. Ing. Lačezar Ličev, CSc.