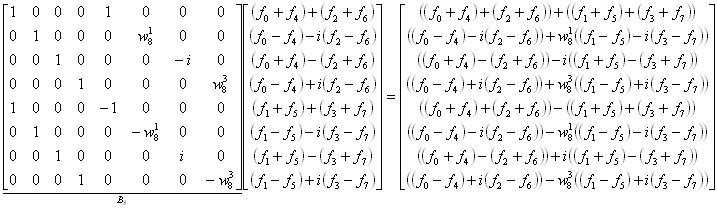Diskrétní Fourierova transformace
Vzpomeňme, že ( viz učební texty k předmětu Integrální transformace) k rekonstrukci
signálu z koeficientů Fourierovy řady v komplexním tvaru
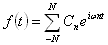 ,
,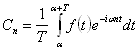
je potřeba pro dosažení téže kvality rekonstruovaného signálu
dvojnásobného počtu koeficientů než při použití Four. řady ve tvaru
reálném

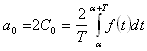


Chceme-li ušetřit výpočtovou kapacitu, zkrátit čas výpočtu, je tedy
výhodnější použít Four. řadu v reálném tvaru. Tato skutečnost
analogicky platí v diskrétní oblasti, kde si jednorozměrnou diskrétní
Four. transformaci (DFT 1) definujeme např.
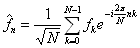
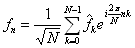
Označíme-li (Uvažujme pouze ortonormální soustavy funkcí. Nedopustíme
se omylu, neboť každou soustavu funkcí lze normalizovat.) 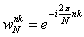 , můžeme psát
, můžeme psát 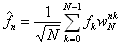
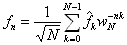
Vytvoříme-li matici, jejíž prvky budou 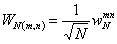 , tedy
, tedy
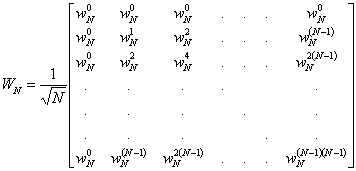
, pak platí 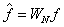 ,
,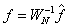
Uvědomíme-li si, že jsme definovali 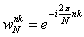 a vzpomeneme-li ( viz Funkce komplexní proměnné), že funkce
a vzpomeneme-li ( viz Funkce komplexní proměnné), že funkce 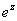 je
je 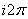 periodická (
periodická (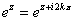 ,
, ,
,
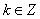 )
můžeme psát např. pro N=8:
)
můžeme psát např. pro N=8:
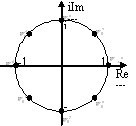
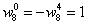
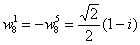
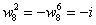
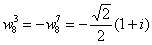
Nakonec tedy dostáváme matici ve tvaru (př. pro N=8 )
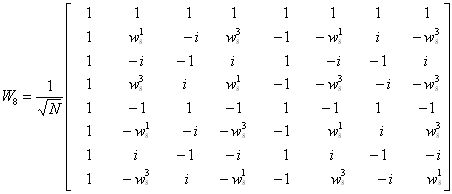
Ze vztahu 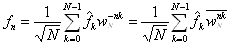 plyne
plyne 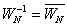 , kde prvky matice
, kde prvky matice 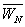 jsou komplexně sdružené s prvky matice
jsou komplexně sdružené s prvky matice 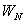 . Při výpočtu dochází
. Při výpočtu dochází 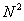 krát k násobení, tudíž tento postup není vhodný tam, kde je potřeba rychle zpracovávat velké množství dat.
krát k násobení, tudíž tento postup není vhodný tam, kde je potřeba rychle zpracovávat velké množství dat.
Příklad:
Uvažujme N=8 a 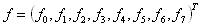 . Pak diskrétní Four. transformace signálu f bude:
. Pak diskrétní Four. transformace signálu f bude:
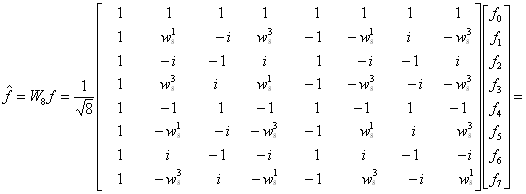
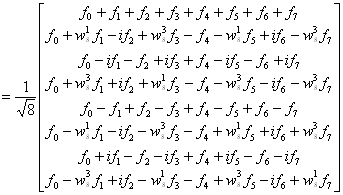
Rychlá Fourierova transformace
FFT - Fast Fourier Transformation
Hledáme-li rychlejší algoritmus výpočtu Four. transformace, můžeme postupovat takto.
(Pouze pro signál, který má 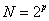 ,
, 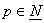 hodnot (vzorků), přičemž
hodnot (vzorků), přičemž 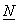 značí množinu přirozených čísel).
značí množinu přirozených čísel).
Rozdělme signál na dvě komponenty:
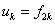
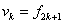 ,
,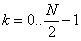 a označme
a označme 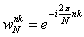 .
.
Fourierova transformace signálu pak bude:
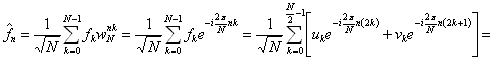
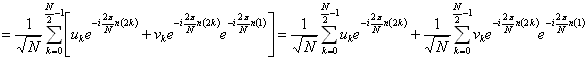
Vzhledem k tomu, že člen 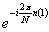 není závislý na hodnotě sumační proměnné k, je možné jej předsunout před sumu:
není závislý na hodnotě sumační proměnné k, je možné jej předsunout před sumu:
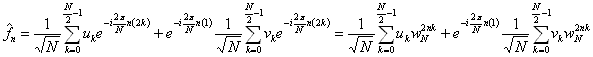
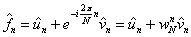
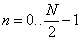

Vztah pro 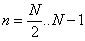 dostaneme obdobně:
dostaneme obdobně:
přeznačme 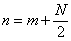 ,
, 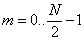
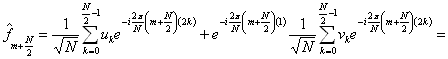
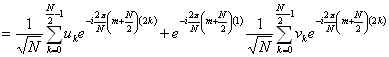
Z periodicity funkce 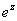 ,
,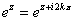 ,
, ,
,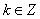 plyne:
plyne:
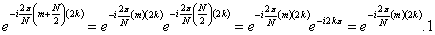
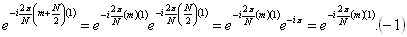
tudíž
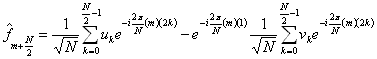
Nyní stačí (není to nutné) místo m psát n, 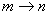
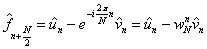
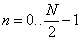

Odvozené vztahy budou v následujícím textu velmi podstatné, proto je zopakujme:
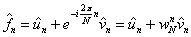
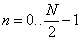

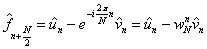
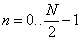

Jak je patrno, rozdělili jsme transformaci přes N bodů na dvě transformace přes N/2 bodů.
Pokud však budeme pokračovat v dělení jednotlivých posloupností vždy na
dvě podle obrázku (zůstaneme u značení vybraných posloupností sudých
členů písmenem u, lichých členů písmenem v), dojdeme do stavu, kdy
výsledná posloupnost bude obsahovat jen 2 prvky.
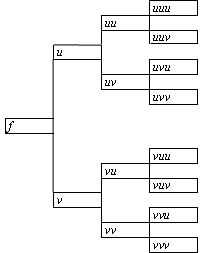
Jejich DFT 1 pak bude:
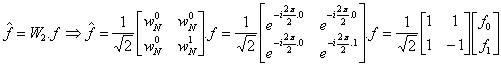
Příklad:
Uvažujme N=8 a 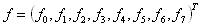 Při rozkladu si pomůžeme obrázkem:
Při rozkladu si pomůžeme obrázkem:
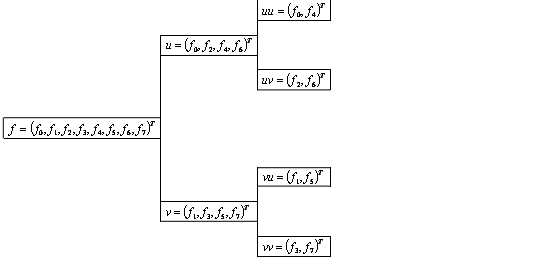
Postup výpočtu by se dal naznačit následujícím schématem:
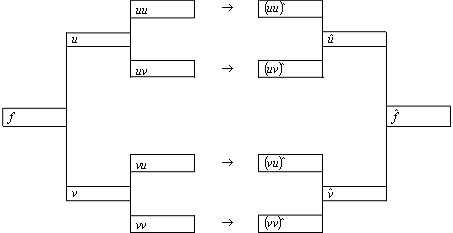
Podrobnější (a složitější) schémata se dají najít v literatuře,
zabývající se detailně diskrétními transformacemi (např. The DFT – An
owner’s manual for the discrete Fourier transform; William L. Briggs,
Van Emden Henson; Siam).
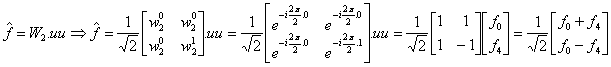
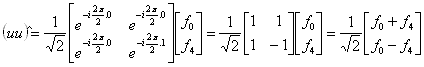
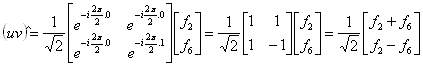
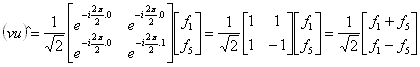
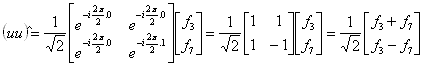
Nyní vzpomeňme na vztahy 
 a aplikujme je:
a aplikujme je:
Opět aplikujeme 
 :
:

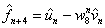
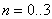
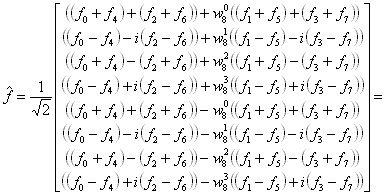
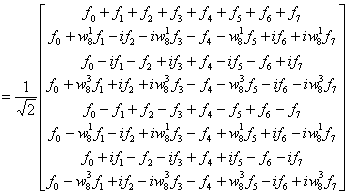
Poměr počtu násobení nutných k výpočtu DFT 1 a FFT 1 je (pokud si vzpomeneme, že 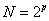 )
)
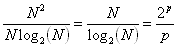
(Důkaz – viz např. Fourier and zavelet analysis; L. Narici, G. Bachman,
E. Beckenstein; Springer, An introduction to wavelets trough linear
algebra; M. W. Frazier; Springer.)
Např. pro p=10 je N=1024 a tedy výpočet FFT 1 je 102,4 krát rychlejší než výpočet DFT 1.
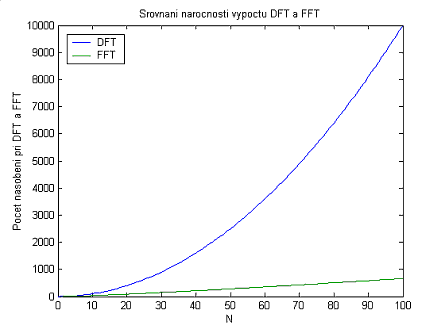
Pokud bychom chtěli využít k počítání FFT 1 maticového zápisu,
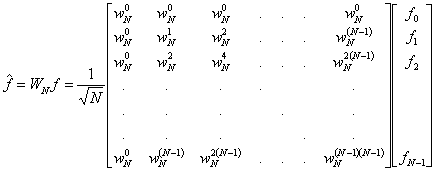
musíme se zabývat otázkou nalezení transformační matice, pro níž by platilo:
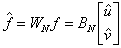 (Matice je označena velkým písmenem B podle obvyklého označování této
metody – Butterfly.) Matice splňující tyto požadavky byla nalezena ve
tvaru
(Matice je označena velkým písmenem B podle obvyklého označování této
metody – Butterfly.) Matice splňující tyto požadavky byla nalezena ve
tvaru 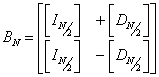 , jde tedy o matici složenou ze submatic, kde
, jde tedy o matici složenou ze submatic, kde 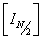 je jednotková matice řádu N/2,
je jednotková matice řádu N/2, 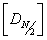 je diagonální matice, kterou lze obecně napsat ve tvaru:
je diagonální matice, kterou lze obecně napsat ve tvaru:
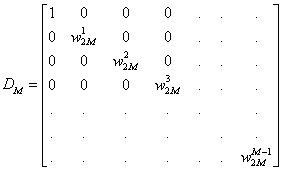
Pak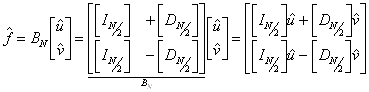 kde
roznásobení matic se řídí pravidly pro násobení matic, přičemž na
submatice nahlížíme jako na prvky klasické matice. Po roznásobení matic
se roznásobení submatic řídí opět pravidly pro násobení matic, kdy již
násobíme přímo jednotlivé prvky submatic.
kde
roznásobení matic se řídí pravidly pro násobení matic, přičemž na
submatice nahlížíme jako na prvky klasické matice. Po roznásobení matic
se roznásobení submatic řídí opět pravidly pro násobení matic, kdy již
násobíme přímo jednotlivé prvky submatic.
Konečný vztah pro FFT 1 signálu délky 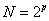 ,
,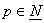 pak je:
pak je:
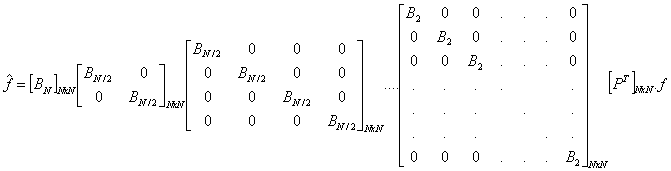

kde 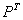 je
permutační matice, která zajišťuje rozdělení vstupní posloupnosti
(signálu) na patřičné vybrané posloupnosti sudých a lichých členů.
Motýlkové matice B neaplikujeme přímo na vstupní signál, ale až na
součin signálu a permutační matice, což odpovídá předchozímu rozkladu
podle obrázku.
je
permutační matice, která zajišťuje rozdělení vstupní posloupnosti
(signálu) na patřičné vybrané posloupnosti sudých a lichých členů.
Motýlkové matice B neaplikujeme přímo na vstupní signál, ale až na
součin signálu a permutační matice, což odpovídá předchozímu rozkladu
podle obrázku.
Vraťme se k předchozímu příkladu (N=8 a 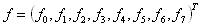 )
)
Snad trochu názorněji by se dalo psát:
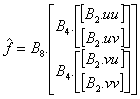 Při výpočtu bychom museli postupovat zevnitř.
Při výpočtu bychom museli postupovat zevnitř.
Postupujme však přesně podle vztahu 
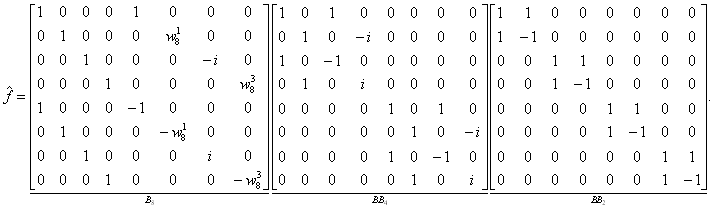
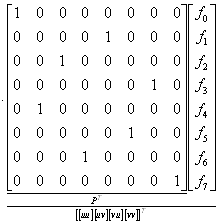

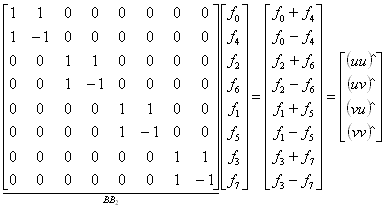
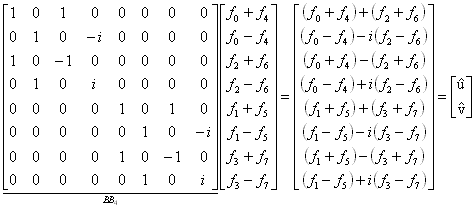
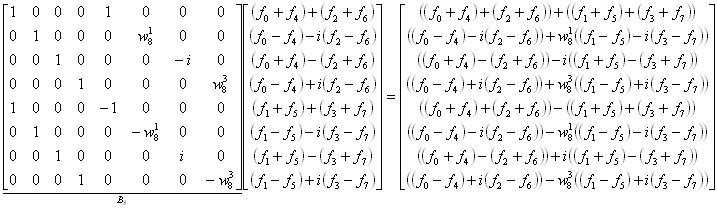
Výsledek můžeme srovnat s výsledky předchozích příkladů.
V každém kroku výpočtu (provádí se zprava) platí (podle 
 ),
že následující posloupnost délky m je vždy kombinací
Fourierových obrazů při DFT 1 předchozích posloupností délky m/2.
),
že následující posloupnost délky m je vždy kombinací
Fourierových obrazů při DFT 1 předchozích posloupností délky m/2.
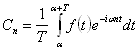
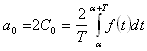
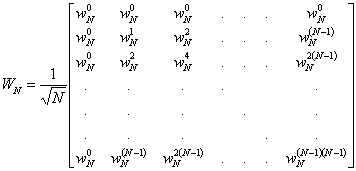

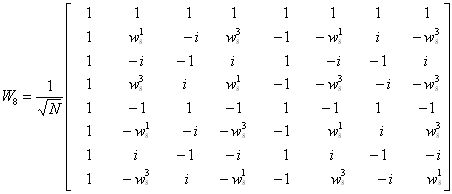
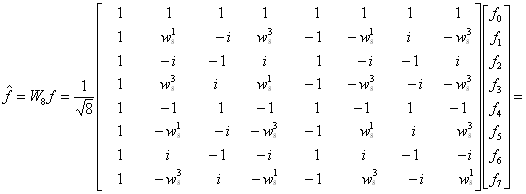
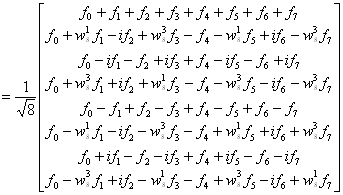
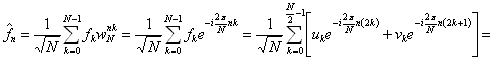
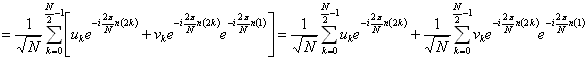
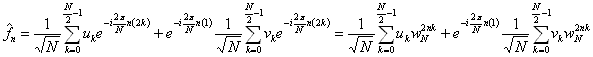
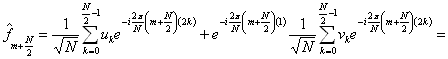
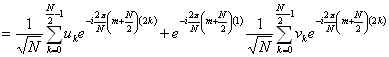
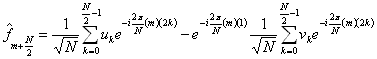

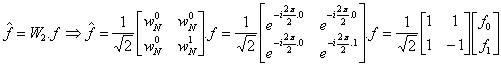


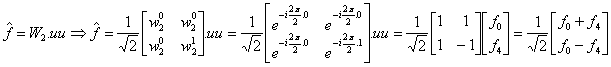
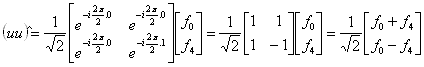
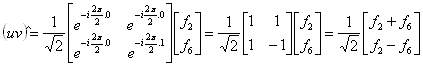
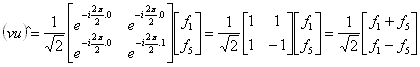
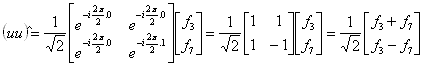
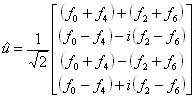
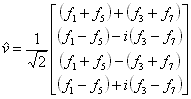
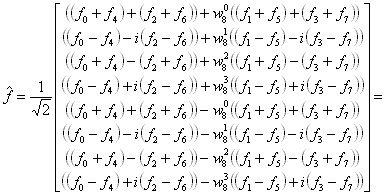
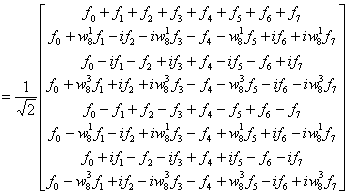

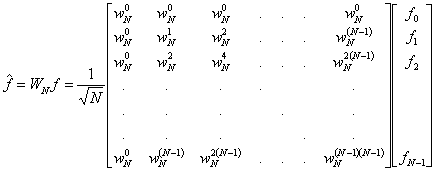
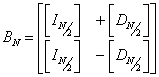 , jde tedy o matici složenou ze submatic, kde
, jde tedy o matici složenou ze submatic, kde 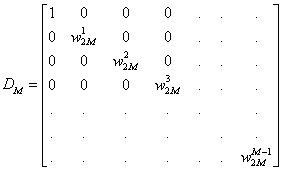
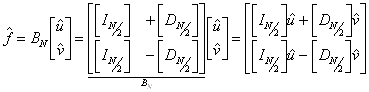 kde
roznásobení matic se řídí pravidly pro násobení matic, přičemž na
submatice nahlížíme jako na prvky klasické matice. Po roznásobení matic
se roznásobení submatic řídí opět pravidly pro násobení matic, kdy již
násobíme přímo jednotlivé prvky submatic.
kde
roznásobení matic se řídí pravidly pro násobení matic, přičemž na
submatice nahlížíme jako na prvky klasické matice. Po roznásobení matic
se roznásobení submatic řídí opět pravidly pro násobení matic, kdy již
násobíme přímo jednotlivé prvky submatic. 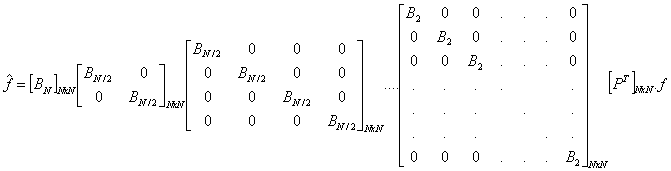
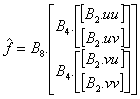 Při výpočtu bychom museli postupovat zevnitř.
Při výpočtu bychom museli postupovat zevnitř.