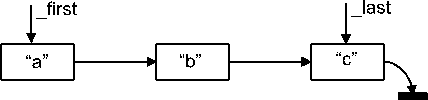
V případě implementace pomocí vázaného seznamu si můžeme udržovat odkaz na první prvek, takže pro odebrání prvku ze začátku fronty nemusíme zbývající prvky přesunovat, ale postačí jen přesměrování odkazu z prvního prvku na druhý. Složitost této operace je tedy konstantní. Pro připojení prvku na konec fronty potřebujeme vyhledat poslední prvek. Pokud budeme postupovat od začátku fronty a přesouvat se směrem vpřed až k poslednímu prvku, bude tato operace vyžadovat počet kroků úměrný délce fronty, takže časová složitost operace vkládání bude lineární. Ovšem opět postačí si pamatovat odkaz na poslední prvek a ten pak připojit jednoduchým přesměrováním odkazů (viz Obr. 3.5). Tato operace má již složitost konstantní.

Obrázek 3.5. Fronta implementovaná jako vázaný seznam

class QueueElem { 
  Object    data;     // hodnota 
  QueueElem next;     // reference na další prvek 
	 
  QueueElem(Object data, QueueElem next) { 
    this.data = data;  
    this.next = next; 
  } 
}
public class LinkedQueue implements Queue 
{ 
  public void enqueue(Object obj) { 
    QueueElem elem = new QueueElem(obj, null); 
    if( _last == null ) 
      _first = elem; 
    else 
      _last.next = elem; 
    _last = elem; 
  } 
 
  public Object dequeue() { 
    assert _first != null : "Fronta je prazdna"; 
    QueueElem elem = _first; 
    _first = elem.next; 
    if( _first == null ) _last = null; 
    return elem.data; 
  } 
 
  public Object front() { 
    assert _first != null : "Fronta je prazdna"; 
    return _first.data;	 
  } 
 
  public boolean empty() { 
    return _first == null; 
  } 
 
  protected QueueElem _first = null; 
  protected QueueElem _last = null; 
}