| Obrázek | Obr. č.1 | Kosinový obraz obrázků |
 |
=> |
 |
| Obr. č.2 | ||
 |
=> |  |
| Obr. č.3 | ||
 |
=> |  |
| Obr. č.4 | ||
 |
=> |  |
| Obr5 | ||
 |
=> |  |
Diskrétní kosinová transformace je speciálním případem diskrétní Fourierovy transformace. Při výpočtu diskrétní Fourierovy transformace dochází (jako v případě transformací spojitých funkcí) k periodickému rozšíření signálu na celou množinu R. Můžeme však záměrně signál rozšířit periodicky tak, že vznikne funkce sudá. Ta je, kromě jiného, vhodná proto, že je spojitá. Při výpočtu Four. koeficientů se pak vyruší sinusové složky a zůstanou pouze složky kosinusové. A toho lze využít ke snížení počtu výpočtů potřebných koeficientů. Chcete vědět víc?
Spektra
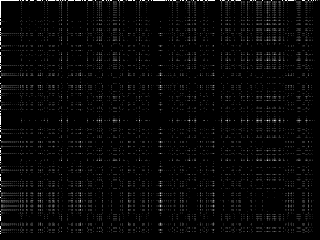
Spektra generovaných obrázků jsou počítána funkcí dct2 v Matlabu. Spektra jsou počítána ze svetělnosti (kanál Y). Kvůli vysoké stejnosměrné složce je tato složka potlačena a pro vyniknutí detailů je celé spektrum vynásobeno koeficientem 2.
| Obrázek | Obr. č.1 | Kosinový obraz obrázků |
 |
=> |
 |
| Obr. č.2 | ||
 |
=> |  |
| Obr. č.3 | ||
 |
=> |  |
| Obr. č.4 | ||
 |
=> |  |
| Obr5 | ||
 |
=> |  |
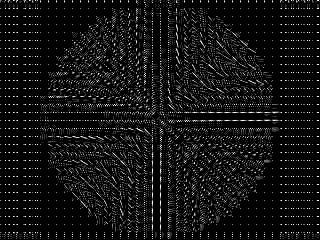
Kosinová spektra podle JPEGu
Je zde pěkně zřetelná jistá lokalizace spektra k místu na obrázku.
| Obrázek | Obr1 | Kosinový obraz obrázků (JPG) |
 |
=> |
 |
| Obr2 | ||
 |
=> |  |
| Obr3 | ||
 |
=> |  |
| Obr4 | ||
 |
=> |  |
| Obr5 | ||
 |
=> | 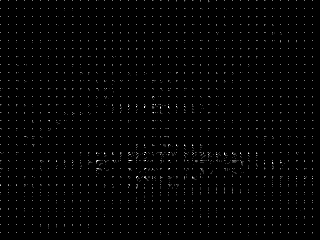 |
Komprese obrázků
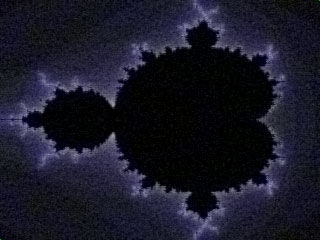
Pro srovnání rozdílů mezi jednotlivými transformacemi jsme sepsali malý prográmek v Matlabu, který komprimoval naše vygenerované obrázky. Pro všechny obrázky jsou nastaveny stejné parametry ( koeficient prahování ). Komprimován je celý obrázek a ne čtverečky 8x8, jak tomu bylo u JPEGu. Proto na obrázcích nejsou artefakty známé z JPEGu.
|
Obr. č.1 před kompresí
|
Obr. č.1po kompresi |
 |
 |
|
Obrázek sestavený ze zahozených koeficientů
|
Statistická data - Matlab
|
 |
Velikost obrázku před kompresí:
1843200 B Velikost obrázku po kompresi: Kompresní poměr: Ušetřené místo v procentech |
Obr. č.2
|
Obr. č.2 před kompresí
|
Obr. č.2 po kompresi |
 |
 |
|
Obrázek sestavený ze zahozených koeficientů
|
Statistická data - Matlab
|
 |
Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: Kompresní poměr: Ušetřené místo v procentech |
Obr. č.3
|
Obr. č.3 před kompresí
|
Obr. č.3 po kompresi |
 |
 |
|
Obrázek sestavený ze zahozených koeficientů
|
Statistická data - Matlab
|
 |
Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: Kompresní poměr: Ušetřené místo v procentech |
Obr. č.4
|
Obr. č.4 před kompresí
|
Obr. č.4 po kompresi |
 |
 |
|
Obrázek sestavený ze zahozených koeficientů
|
Statistická data - Matlab
|
 |
Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: Kompresní poměr: Ušetřené místo v procentech |
|
Obr. č.5 před kompresí
|
Obr. č.5 po kompresi |
 |
 |
|
Obrázek sestavený ze zahozených koeficientů
|
Statistická data - Matlab
|
 |
Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: Kompresní poměr: Ušetřené místo v procentech |
Výpis programu v Matlabu:
Závěrem:
Jak je vidět, tak DCT transformace a na ní postavená komprese poskytuje velmi dobré kompresní možnosti. Data v naší ukázkové kompresi jsou sice zajímavá, ale je nutné si uvědomit že velikosti v naší tabulce postrádají jakoukoliv hlavičku. Pro formát "schopný života" by nároky na paměťové místo vzrostly asi tak dvojnásobně.(Hlavička souboru+ režijní informace)