Teorie:

Podobně jako v oblasti signálů spojitých, je možné i v oblasti signálů diskrétních definovat transformaci, která bude diskrétní obdobou Fourierovy transformace ve spojité oblasti. Tuto transformaci nazýváme Discrete Fourier Transform - DFT - Diskrétní Fourierova Transformace.Ale vzhledem k tomu, že výpočet DFT vyžaduje značný počet násobení ( ), což je časově nejnáročnější operace, byl vyvinut algoritmus, umožňující značné urychlení výpočtu. Tento algoritmus je označován Fast Fourier Transform - FFT - Rychlá Fourierova Transformace.

Chcete vědět víc?

Spektra

Spektra generovaných obrázků jsou počítána funkcí FFT v Matlabu. Spektra jsou počítána ze svetělnosti (kanál Y). Kvůli vyniknutí detailů jsou ve spektrech dělány úpravy ( snížení jasu ). Jsou zde vykreslena "jednostraná" amplitudová a fázová spektra. Z estetického hlediska jsem zde také přidal přímo výsledek FFT z Matlabu. FFT počítá i záporné frekvenční pásmo, ale to je z důvodu symetrie spekter je stejné jako kladné frekvenční pásmo. Z tohoto důvodu není potřeba uchovávat tyto informace.

Obrázek	Obr. č.1	Frekvenční obraz obrázků
	=>	celé amplitudové spektrum Amplitudové spektrum Fázové spektrum
Obrázek	Obr. č.2	Frekvenční obraz obrázků
	=>	celé amplitudové spektrum Amplitudové spektrum Fázové spektrum
Obrázek	Obr. č.3	Frekvenční obraz obrázků
	=>	celé amplitudové spektrum Amplitudové spektrum Fázové spektrum
Obrázek	Obr. č.4	Frekvenční obraz obrázků
	=>	celé amplitudové spektrum Amplitudové spektrum Fázové spektrum
Obrázek	Obr. č.5	Frekvenční obraz obrázků
	=>	celé amplitudové spektrum Amplitudové spektrum Fázové spektrum

fft_obraz.zip

Komprese obrázků

Pro kompresi těchto obrázků jsme kvůli objektivnímu posouzení z hlediska transformací využili stejný algoritmus jako u komprese s využitím DCT. Pro všechny obrázky je opět stejné nastavení. U této transformace by se dal algoritmus trochu modifikovat k dosažení lepších kompresních poměrůdíky symetrii frekvenčního spektra

Obr. č.1

Obr. č.1 před kompresí	Obr. č.1 po kompresi
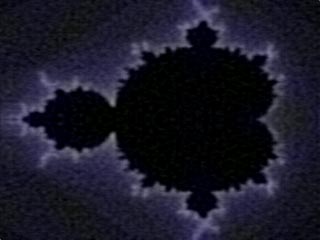Obrázek sestavený ze zahozených koeficientů	Statistická data - Matlab
	Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: 46640 B Kompresní poměr: 1 : 39.5197 Ušetřené místo v procentech 97.46962%

Obr. č.2

Obr. č.2 před kompresí	Obr. č.2 po kompresi
Obrázek sestavený ze zahozených koeficientů	Statistická data - Matlab
	Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: 258960 B Kompresní poměr: 1 : 7.117702 Ušetřené místo v procentech 85.95052%

Obr. č.3

Obr. č.3 před kompresí	Obr. č.3 po kompresi
Obrázek sestavený ze zahozených koeficientů	Statistická data - Matlab
	Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: 26928 B Kompresní poměr: 1 : 68.4492 Ušetřené místo v procentech 98.53906%

Obr. č.4

Obr. č.4 před kompresí	Obr. č.4 po kompresi
Obrázek sestavený ze zahozených koeficientů	Statistická data - Matlab
	Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: 6544 B Kompresní poměr: 1 : 281,6626 Ušetřené místo v procentech 99,64497%

Obr. č.5

Obr. č.5 před kompresí	Obr. č.5 po kompresi
Obrázek sestavený ze zahozených koeficientů	Statistická data - Matlab
	Velikost obrázku před kompresí: 1843200 B Velikost obrázku po kompresi: 9520 B Kompresní poměr: 1 : 193,6134 Ušetřené místo v procentech 99,48351%

Výpis programu v Matlabu:

komprese_fft.zip

Závěrem:

Mnohým z Vás jistě neunikla ta podobnost spekter kosinové transformace s Fourierovou transformaci. Je to dáno tím, že kosinová transformace je speciálním případem Fourierovy transformace v reálném tvaru. Viz. DCT 

Kaľdý krok je hodnocen nezávisle.

Prezentace a cvičení převzaté od Leoše Maršálka a Jana Skapy © 2003, upravil doc. Ing. Lačezar Ličev, CSc.